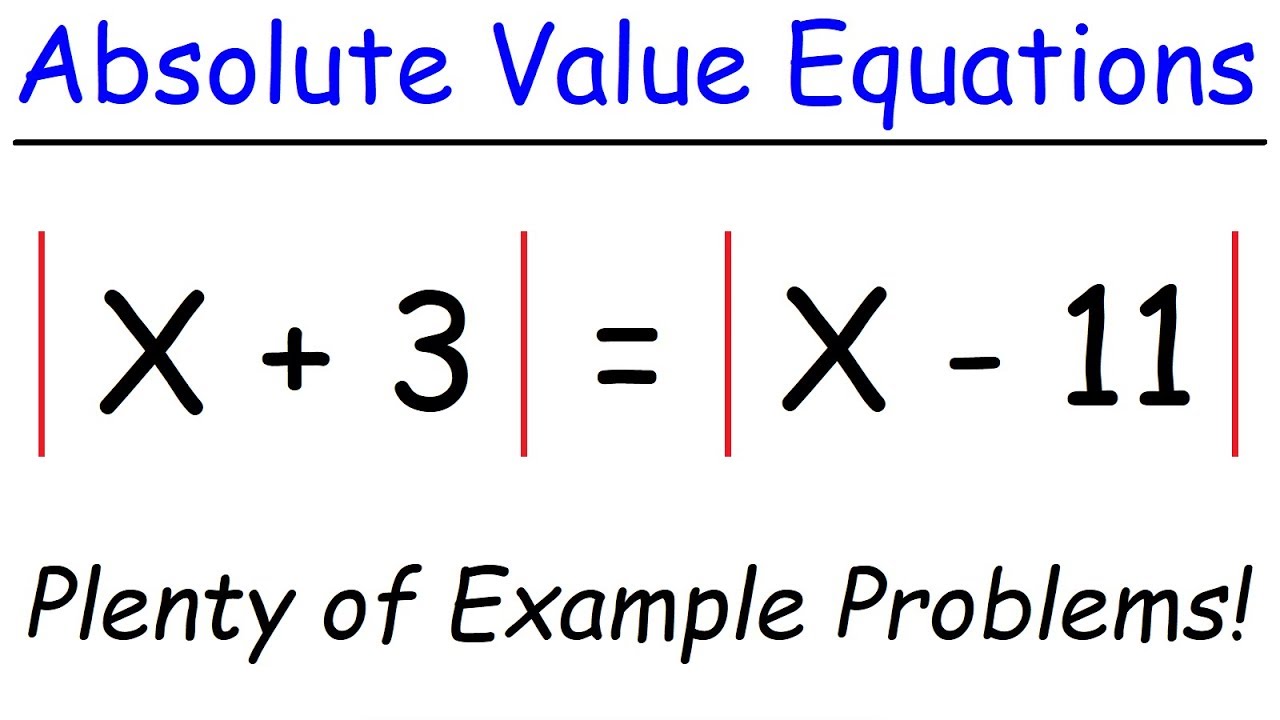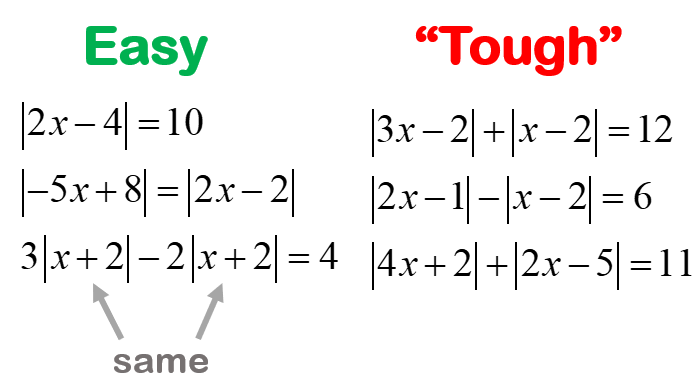How to Effectively Find Absolute Value: A Practical Guide for 2025
Understanding the absolute value is fundamental in mathematics, providing crucial insight into topics like equations, inequalities, and functions. This guide will explore the definition of absolute value, methods to find it, and its practical applications—all to help enhance your understanding of this concept in mathematics for 2025.
What Is Absolute Value?
The absolute value of a number refers to its distance from zero on the number line, regardless of its sign. In mathematical terms, the absolute value of a number \( x \) is denoted as \( |x| \). Therefore, whether a number is positive or negative, its absolute value will always be non-negative. For instance, both -5 and +5 have an absolute value of 5 because they are both 5 units away from zero. This fundamental concept plays a significant role in various math problems and is essential for solving absolute value equations and inequalities.
Understanding Absolute Value by Examples
To enhance your comprehension of absolute value, let’s look at some examples. The absolute value function displays various characteristics; for example, any negative integer will return a positive value when its absolute value is calculated. If we take the absolute value of -8, \( |-8| = 8 \), while for positive integers, such as 3, \( |3| = 3 \). Such evaluations are foundational in subjects like algebra, where students frequently deal with absolute value in mathematics and its rules.
Graphing Absolute Values
A useful way to visualize absolute value is through graphing. The graph of the absolute value function, \( y = |x| \), forms a “V” shape when plotted on a Cartesian plane. For instance, on this graph, any point represents a y-value equivalent to the x-value’s absolute value. Understanding this graphing technique can help students better grasp absolute value concepts and how they apply to other mathematical operations.
How to Find Absolute Value
Finding absolute value can be accomplished through various methods, depending on the complexity of the problem at hand. Below are some practical approaches commonly utilized to find the absolute value of different types of numbers, such as fractions and negative integers, which align with mathematical operations.
Finding the Absolute Value of Negative Numbers
One common inquiry involves calculating the absolute value of negative numbers. To find this, simply identify the number’s magnitude without its negative sign. For example, to find the absolute value of -9, you would note that \( |-9| = 9 \). By consistently applying this method, learners can quickly gain confidence in solving before moving on to more challenging problems.
Finding the Absolute Value of Fractions
The absolute value of a fraction is computed similarly to that of integers. For example, \( |-3/4| = 3/4 \). Regardless of whether the fraction is negative or positive, the result remains a positive value, disallowing a negative sign from affecting the computation. Understanding this technique fosters proficiency in handling absolute value practice problems involving various types of numbers.
Properties of Absolute Value
Mastering the properties of absolute value aids in simplifying complex mathematical challenges. These properties can be especially valuable when tackling equations and inequalities in higher-level mathematics.
Properties Highlighted in Absolute Value Operations
There are a few critical properties to consider when working with absolute value:
- Non-negativity: The absolute value of any number is never negative. For example, \( |5| = 5 \) and \( |-5| = 5 \).
- Multiplicative Property: The absolute value of the product of numbers is the product of their absolute values: \( | ab | = |a| \cdot |b| \).
- Additive Property: For any real numbers \( a \) and \( b \), \( |a + b| ≤ |a| + |b| \). This means the absolute value of a sum is less than or equal to the sum of their absolute values, a principle often useful in inequalities.
Incorporating these properties into problem solving enhances a learner’s ability to tackle complex absolute value equations accurately.
Common Mistakes in Understanding Absolute Value
While exploring the absolute value, individuals may encounter common misconceptions. One frequent error is assuming that \( |a + b| \) equals \( |a| + |b| \). In reality, this is only the case under specific conditions. Understanding these common pitfalls encourages better performance in mathematical tasks and greater success in overcoming challenges pertaining to absolute value.
Applications of Absolute Value
Outside the classroom, the importance of absolute value extends to several practical applications in daily life. Familiarizing oneself with these applications can aid students in grasping the significance of this mathematical concept.
Real World Examples of Absolute Value
Absolute value finds many real-world applications, particularly in fields such as engineering, physics, and even finance, where the concept of absolute distance can be crucial. For instance, in risk assessment in finance, analysts might consider absolute changes in value, disregarding direction, thus requiring a solid grasp of how to find and apply absolute values effectively.
Using Absolute Value in Mathematical Challenges
Embracing the challenge of solving absolute value problems encourages deeper understanding. Teachers might implement engaging exercises that allow students to apply their knowledge of absolute values, thus solidifying absolute value concepts. These approaches promote a positive learning atmosphere and help enrich the educational experience.
Key Takeaways
- Understanding absolute value is crucial for solving mathematical problems related to equations and inequalities.
- Identifying absolute value of negative integers and fractions using straightforward methods is fundamental for math competency.
- Mastering the properties of absolute value enhances skills in dealing with complex mathematical tasks.
- Real-world applications illustrate the necessity of grasping absolute value in practical scenarios.
- Continued practice with absolute value exercises solidifies knowledge and aids in identifying and addressing common mistakes.
FAQ
1. What is the absolute value of a number?
The absolute value of a number is its distance from zero on the number line. It represents how far the number is from zero, regardless of its sign. For instance, both \( |3| \) and \( |-3| \) equal 3 because they have the same distance from zero.
2. How is absolute value used in algebra?
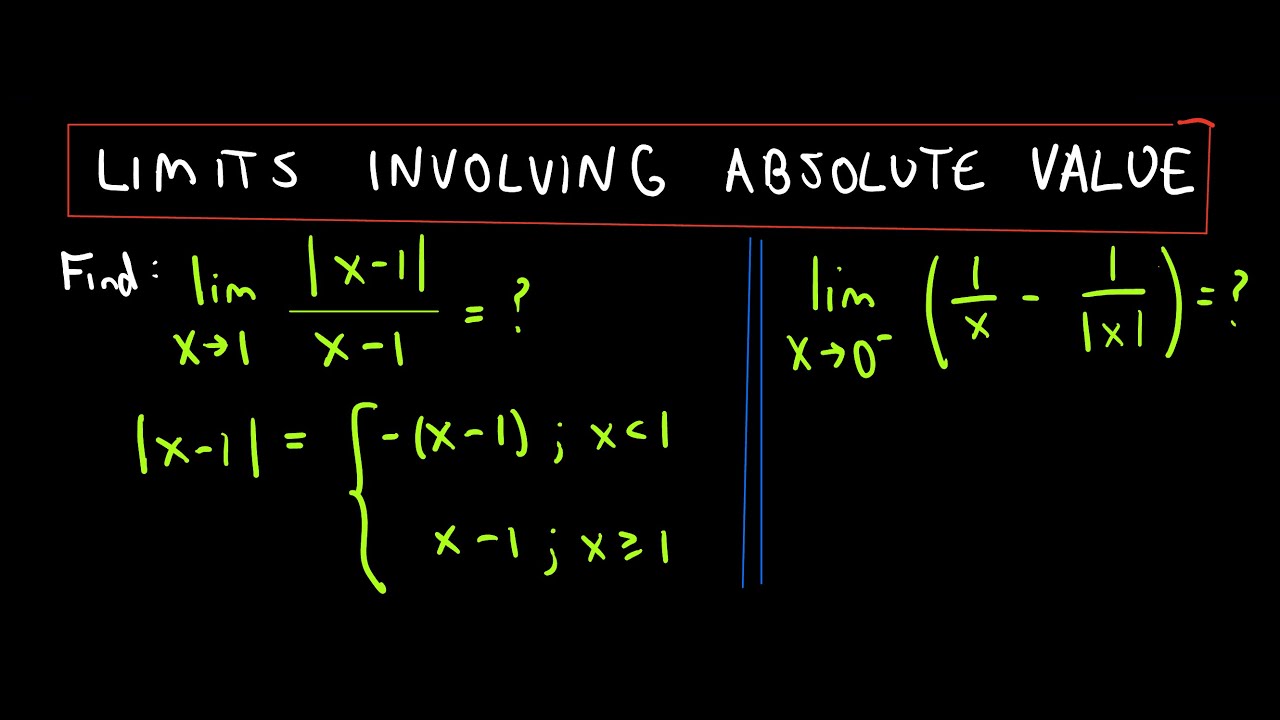
In algebra, absolute value is used extensively in solving equations and inequalities. For instance, when you solve for \( |x – 5| = 3 \), you must address two cases: \( x – 5 = 3 \) and \( x – 5 = -3 \). This utilization aids in dissecting problems to find possible solutions.
3. Can absolute value be applied to fractions?
Yes, you can find the absolute value of fractions in the same way as integers. For example, \( |-2/3| = 2/3 \). Regardless of whether the fraction is positive or negative, applying the absolute value produces a non-negative result, reflecting its distance from zero.
4. What are some real-world applications of absolute value?
Absolute value has practical applications in various fields. For example, in finance, it’s used to analyze the absolute changes in investment values, disregarding direction. In physics, it’s employed to measure distances, regardless of whether they are positive or negative.
5. How can I practice problems involving absolute value?
To practice absolute value problems, engage with educational resources such as worksheets or online quizzes focused on absolute value concepts. These exercises will enhance your understanding and proficiency in tackling both simple and complex absolute value challenges.
Further Learning Resources
If you’re eager to expand your knowledge further, check out additional resources, like mathematical tutorials and exercises focused on absolute value. Engaging with interactive platforms can also enrich your understanding. Use this guide not just as a reference point but as a stepping stone to mastering absolute values in mathematics.