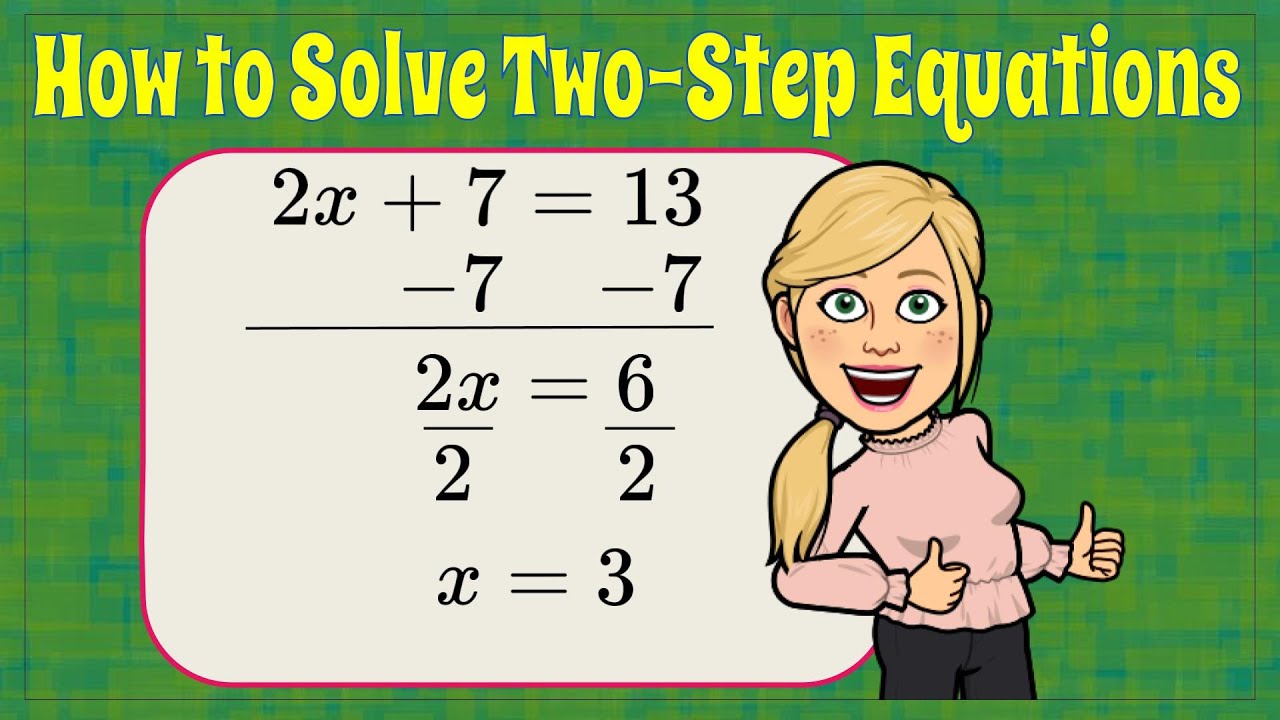Effective Ways to Solve Two-Step Equations and Improve Your Math Skills in 2025

Understanding and solving two-step equations is a foundational skill in algebra that significantly enhances your overall math skills. By mastering this technique, you can tackle more complex algebraic equations with confidence. In this article, we will explore effective strategies for solving two-step equations, practical examples, and tips for improving your math abilities.

Understanding Two-Step Equations

Two-step equations are algebraic expressions that require two operations to isolate the variable. They often take the form ax + b = c. The goal is to solve for x by performing the necessary mathematical operations in the correct order. Understanding how to isolate the variable is crucial in learning how to manipulate various equation forms.

Types of Two-Step Equations

Two-step equations can appear in different forms, often involving both addition and subtraction or multiplication and division. For example, if you have the equation 3x + 5 = 20, you will first need to use the subtraction method to eliminate the constant (5) and then apply the multiplication method to solve for x. This highlights the importance of being able to identify different equation types and the operations involved.

Key Components of Two-Step Equations

Two-step equations comprise various elements such as the coefficient (the number multiplying the variable), the constant (the number added or subtracted), and the variable itself. By learning to identify and manipulate these components using methods like the addition method and the subtraction method, you can simplify equations effectively.

Step-by-Step Instructions for Solving

A systematic approach to solving two-step equations involves the following steps:
1. **Identify the operations**: Look for what’s being done to the variable.
2. **Use inverse operations**: If the variable is being added to a constant, use subtraction; if multiplied, use division.
3. **Balance the equation**: Whatever operation is applied to one side must be applied to the other to maintain equality.
4. **Isolate the variable**: Continue operating until the variable stands alone.
5. **Check your solution**: Substitute the value back into the original equation to verify accuracy.

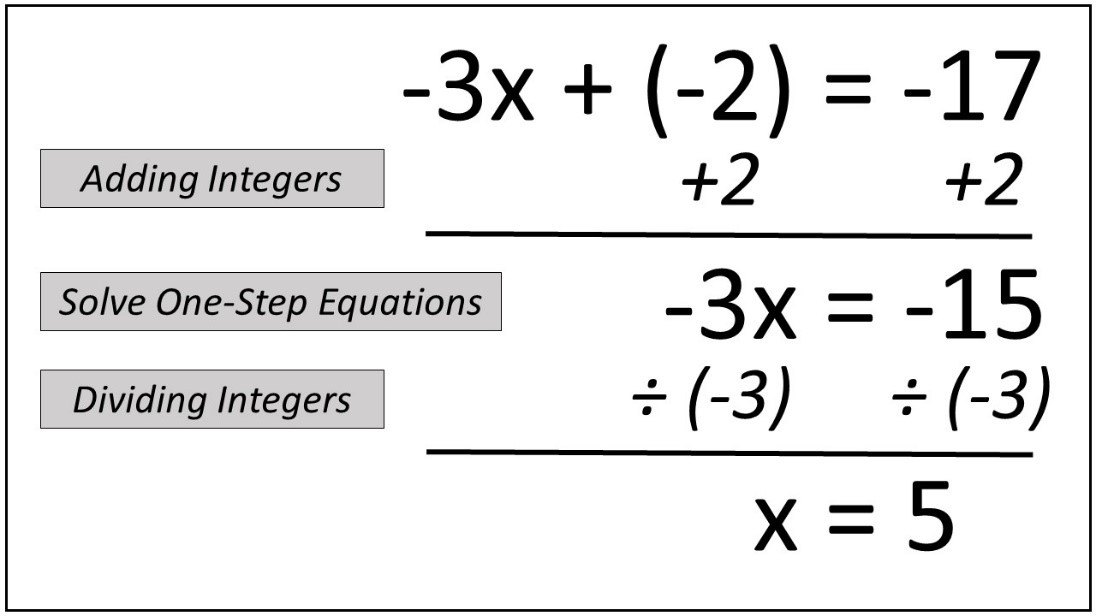
Effective Methods for Teaching Two-Step Equations

Teaching two-step equations requires the right resources and strategies to ensure students grasp the concepts effectively. Using educational resources, such as interactive learning tools and collaborative activities, can enhance student engagement and learning.

Using Visual Aids

Visual representations can help students better grasp the concept of equation balance. Tools such as graphs can illustrate how equations function and relate to each other. Utilizing math games or math worksheets reinforces learning through repetition and practice, essential in building a solid foundation in algebra.

Integrating real-life applications

One way to enhance problem-solving skills is by applying sophisticated equation applications to everyday problems. For instance, you can illustrate how equations in economics or equations in physics are utilized. Case studies or word problems can make learning more relatable and highlight the importance of understanding linear equations and their real-world implications.

Assessment Techniques

Instructors can assess student understanding through regular evaluations that include practice problems, quizzes, and collaborative projects. Leveraging online resources for homework help or using educational videos can greatly aid in reinforcing students’ understanding of algebra basics.

Exploring Advanced Strategies for Two-Step Equations

Once you’ve mastered basic two-step equations, you can explore more complex solving techniques that involve multi-step equations and the handling of fractions.

Multi-Step Equations

Multi-step equations build on the principles of two-step equations but introduce more variables and operations. Solving them requires balanced manipulation across several steps using substitution and inverse operations, similar to the strategies employed in solving for x previously.

Dealing with Fractions

Fractions can make equations seem more daunting, but mastering the equation simplification process makes them manageable. Multiplying through by the least common denominator can help eliminate fractions, making the equations simpler to solve.

Equation Graphing

Graphing equations provides a visual representation of solutions. Understanding how to plot points and interpret graph lines lets students see the relationship between variables clearly. This reinforces algebraic concepts and prepares students for higher-level math challenges.

Concluding Insights and Resources

To excel at solving two-step equations, practice is key. Acquiring knowledge through mathematics tutorials, engaging in real-life equations, and utilizing problem-solving frameworks will enhance your math skills significantly. Students can work independently or collaboratively to strengthen their understanding of equation manipulation and ensure they reach their academic goals.

Key Takeaways

• Solving two-step equations requires understanding operations and using inverse operations effectively.
• Visual aids and real-world applications play a crucial role in comprehending algebraic concepts.
• Advanced strategies, including multi-step equations and dealing with fractions, enhance problem-solving capabilities.
• Utilizing various educational resources further supports learning and reinforces key algebra skills.

FAQ

1. What are the steps to solve two-step equations?

The key steps include identifying the operations on the variable, applying inverse operations to isolate it, maintaining equation balance, and checking your solutions. It’s a systematic approach that reinforces understanding of mathematical principles.

2. How can I check if my solutions are accurate?

You can verify your solutions by substituting your found value back into the original equation. If both sides equal, your solution is accurate. This step is essential in confirming understanding of equation proofs.

3. What role do like terms play in solving equations?

Combining like terms simplifies equations significantly and makes it easier to isolate the variable. It’s crucial in expanding and simplifying expressions in the equation manipulation process.

4. Are there any recommended online resources for practicing two-step equations?

Yes, several online resources provide practice problems, instructional videos, and interactive learning tools tailored for mastering solving equations. Websites like Khan Academy and educational apps grant free access to extensive practice.

5. How can I improve my problem-solving skills in algebra?

To enhance your problem-solving skills, regularly practice different types of problems, engage in collaborative learning, and seek help from educational resources. Monitoring your progress and understanding through consistent self-assessment can also help.

6. What are some strategies for teaching two-step equations?

Utilizing real-life applications, visual aids, and collaborative learning activities can make lessons on two-step equations more engaging. Incorporating games or technology into lessons can also increase student interest in algebra.